GEOMETRÍA Y TRIGONOMÉTRICA

GEOMETRÍA 

Alegoría de la geometría

La geometría (del latín geometrĭa, y este del griego γεωμετρία de γῆ gē, ‘tierra’, y μετρία metría, ‘medida’) es una rama de la matemáticaque se ocupa del estudio de las propiedades de las figuras en el plano o el espacio,¹​ incluyendo: puntos, rectas, planos, politopos (que incluyen paralelas, perpendiculares, curvas, superficies, polígonos, poliedros, etc.).

Es la base teórica de la geometría descriptiva o del dibujo técnico. También da fundamento a instrumentos como el compás, el teodolito, el pantógrafo o el sistema de posicionamiento global (en especial cuando se la considera en combinación con el análisis matemático y sobre todo con las ecuaciones diferenciales).

Sus orígenes se remontan a la solución de problemas concretos relativos a medidas. Tiene su aplicación práctica en física aplicada, mecánica, arquitectura, geografía, cartografía, astronomía, náutica, topografía, balística etc. Y es útil en la preparación de diseños e incluso en la elaboración de artesanía.

Historia[editar]

Artículo principal: Historia de la geometría

Fragmentos de los Elementos de Euclides en los Papiros de Oxirrinco.

La geometría es una de las ciencias más antiguas. Inicialmente está constituida en un cuerpo de conocimientos prácticos en relación con las longitudes, áreas y volúmenes. La civilización babilónica fue una de las primeras culturas en incorporar el estudio de la geometría. La invención de la rueda abrió el camino al estudio de la circunferencia y posteriormente al descubrimiento del número π(pi); También desarrollaron el sistema sexagesimal, al conocer que cada año cuenta con 360 días, además implementaron una fórmula para calcular el área del trapecio rectángulo.²​ En el Antiguo Egipto estaba muy desarrollada, según los textos de Heródoto, Estrabón y Diodoro Sículo. Euclides, en el siglo III a. C. configuró la geometría³​ en forma axiomática y constructiva, tratamiento que estableció una norma a seguir durante muchos siglos: la geometría euclidiana descrita en Los Elementos.

El estudio de la astronomía y la cartografía, tratando de determinar las posiciones de estrellas y planetas en la esfera celeste, sirvió como importante fuente de resolución de problemas geométricos durante más de un milenio. René Descartes desarrolló simultáneamente el álgebra de ecuaciones y la geometría analítica, marcando una nueva etapa, donde las figuras geométricas, tales como las curvas planas, podrían ser representadas analíticamente, es decir, con funciones y ecuaciones. La geometría se enriquece con el estudio de la estructura intrínseca de los entes geométricos que analizan Euler y Gauss, que condujo a la creación de la topología y la geometría diferencial.

Axiomas, definiciones y teoremas[editar]

Un teorema descubierto y probado por Arquímedes: una esfera tiene ²⁄₃ del volumen de su cilindrocircunscrito.

La geometría se propone ir más allá de lo alcanzado por la intuición. Por ello, es necesario un método riguroso, sin errores; para conseguirlo se han utilizado históricamente los sistemas axiomáticos. El primer sistema axiomático lo establece Euclides, aunque era incompleto. David Hilbert propuso a principios del siglo XX otro sistema axiomático, éste ya completo. Como en todo sistema formal, las definiciones, no sólo pretenden describir las propiedades de los objetos, o sus relaciones. Cuando se axiomatiza algo, los objetos se convierten en entes abstractos ideales y sus relaciones se denominan modelos.

Esto significa que las palabras "punto", "recta" y "plano" deben perder todo significado material. Cualquier conjunto de objetos que verifique las definiciones y los axiomas cumplirá también todos los teoremas de la geometría en cuestión, y sus relaciones serán virtualmente idénticas al del modelo tradicional.

Axiomas[editar]

La geometría esférica es un ejemplo de geometría no euclidiana

En geometría euclidiana, los axiomas y postulados son proposiciones que relacionan conceptos, definidos en función del punto, la recta y el plano. Euclides planteó cinco postulados y fue el quinto (el postulado de paralelismo) el que siglos después —cuando muchos geómetras lo cuestionaron al analizarlo— originará nuevas geometrías: la elíptica (geometría de Riemann) o la hiperbólica de Nikolái Lobachevski.

En geometría analítica, los axiomas se definen en función de ecuaciones de puntos, basándose en el análisis matemático y el álgebra. Adquiere otro nuevo sentido hablar de puntos, rectas o planos. f(x) puede definir cualquier función, llámese recta, circunferencia, plano, etc.

Topología y geometría[editar]

El nudo de trébol

El campo de la topología, que tuvo un gran desarrollo en el siglo XX, es en sentido técnico un tipo de geometría transformacional, en que las transformaciones que preservan las propiedades de las figuras son los homeomorfismos (por ejemplo, esto difiere de la geometría métrica, en que las transformaciones que no alteran las propiedades de las figuras son las isometrías). Esto ha sido frecuentemente expresado en la forma del dicho: "la topología es la geometría de la página de goma".

Tipos de geometría[editar]

Desde los antiguos griegos, ha existido numerosas contribuciones a la geometría, particularmente a partir del siglo XVIII. Eso ha hecho que proliferen numerosas subramas de la geometría con enfoques muy diferentes. Para clasificar los diferentes desarrollos de la Geometría moderna se pueden recurrir a diferentes enfoques:

Geometrías según el tipo de espacio[editar]

Los antiguos griegos manejaban un único tipo de geometría, a saber, la geometría euclídea, hábilmente codificada en los Elementos de Euclides por una escuela alejandrina encabezada por Euclides. Este tipo de geometría se basó en un estilo formal de deducciones a partir de cinco postulados básicos. Los cuatro primeros fueron ampliamente aceptados y Euclides los usó extensivamente, sin embargo, el quinto postulado fue menos usado y con posterioridad diversos autores trataron de demostrarlo a partir de los demás, la imposibilidad de dicha deducción llevó a constatar que junto con la geometría euclídea existían otros tipos de geometrías en que el quinto postulado de Euclídes no participaba. De acuerdo a las modificaciones introducidas en ese quinto postulado se llega a familias diferentes de geometrías o espacios geométricos diferentes entre ellos:

• La geometría absoluta, que es el conjunto de hechos geométricos derivables a partir únicamente de los primeros cuatro postulados de Euclides.
• La geometría euclídea, que es la geometría particular que se obtiene de aceptar como axioma también el quinto postulado. Los griegos consideraron dos variantes de geometría euclídea:
  • Geometría euclídea del plano
  • Geometría euclídea del espacio
• La geometría clásica es una recopilación de resultados para las geometrías euclídeas.

A partir del siglo XIX se llegó a la conclusión de que podían definirse geometrías no euclídeas entre ellas:

• La geometría elíptica
• La geometría esférica
• La geometría finita
• La geometría hiperbólica
• La geometría riemanniana

Geometrías asociadas a transformaciones[editar]

En el siglo XIX se constató que otra forma de enfocar los conceptos geométricos era estudiar la invarianza de ciertas propiedades bajo diferentes tipos de transformaciones matemáticas, así se clasificaron diversas propiedades geométricas en grupos y se plantearon subdisciplinas consistentes en ver cuales eran las propiedades invariantes bajo tipos particulares de transformaciones, así aparecieron los siguientes tipos de enfoques geométricos:

• Geometría afín
• Geometría conforme
• Geometría convexa
• Geometría discreta
• Geometría de incidencia
• Geometría ordenada
• Geometría proyectiva

Geometría según el tipo de representación[editar]

Si bien Euclides básicamente se restringió a conceptos geométricos representables mediante figuras (puntos, líneas, círculos, etc.) el desarrollo de otras ramas de las matemáticas no conectadas inicialmente con la geometría propiamente dicha, llevó a poder aplicar las herramientas de otras ramas a problemas propiamente geométricos así nacieron:

• La geometría algebraica
• La geometría analítica
• La geometría descriptiva
• La Topología geométrica
• La geometría diferencial que engloba como ramas a:
  • Geometría diferencial discreta
  • La geometría de curvas y superficies
    • La Geometría diferencial de curvas
    • La Geometría diferencial de superficies
  • La Geometría diferencial de hipersuperficies
  • Geometría diferencial de variedades
  • La geometría de Riemann
• La Geometría fractal
• Geometría sintética

Aplicaciones geométricas[editar]

Además de las subramas propiamente dichas modernamente han surgido numerosas aplicaciones prácticas de la geometría entre ellas:

• • Geometría computacional
  • Geometría constructiva de sólidos
  • Geometría molecular

Enseñanza y aprendizaje de la geometría[editar]

El aprendizaje de la geometría implica el desarrollo de habilidades visuales y de argumentación.

Para que el aprendizaje de la geometría no carezca de sentido, es importante que el grupo docente se preocupe por buscar un equilibrio entre la asociación de habilidades de visualización y argumentación, pues ambas habilidades son fundamentales dentro del proceso formativo del individuo. Es decir, no se trata sólo de enseñar contenidos como una “receta” o por cumplir con lo estipulado en el currículo sino que se pretende que con la enseñanza de la geometría el estudiantado aprenda a pensar lógicamente.⁴​

El ser humano, desde su infancia, crea representaciones del mundo físico que le rodea. Estas le generan una necesidad (teórica y práctica) para lograr el entendimiento de ese mundo. El hemisferio derecho del cerebro resulta ser el más beneficiado ante la presencia de estímulos visuales, a diferencia del hemisferio izquierdo, que tiene la responsabilidad de desarrollar las capacidades verbales. El estudio de la geometría contribuye significativamente al desarrollo de esas necesidades espaciales de visualización; sin embargo, hasta una época histórica reciente, que data a partir de la década de los años 50, es cuando educadores matemáticos se interesaron por el estudio de dicho campo, al vincular la capacidad matemática con la capacidad espacial.⁵​

Respecto a las dificultades que las estudiantes y los estudiantes presentan al estudiar geometría se encuentran: resolver un problema algebraicamente; calcular perímetros, áreas y volúmenes, debido a que no identifican cuál fórmula aplicar y dificultad para interpretar qué es lo que dice un problema. Al realizar el análisis por nivel, se puede observar que en el ciclo diversificado (décimo y undécimo año) la principal dificultad que presentan es interpretar lo que dice un problema. La principal dificultad de las alumnas y alumnos de séptimo, octavo y noveno año, es, respectivamente, comprender las fórmulas del perímetro, áreas y volúmenes y aprender las definiciones; resolver una situación problema algebraicamente y dificultad para extraer información de un dibujo geométrico

Trigonometría

Representación gráfica de un triángulo rectángulo en un sistema de coordenadas cartesianas.

La trigonometría es una rama de la matemática, cuyo significado etimológico es 'la medición de los triángulos'. Deriva de los términos griegos τριγωνοϛ trigōnos 'triángulo' y μετρον metron 'medida'.¹​

En términos generales, la trigonometría es el estudio de las razones trigonométricas: seno, coseno, tangente, cotangente, secante y cosecante. Interviene directa o indirectamente en las demás ramas de la matemática y se aplica en todos aquellos ámbitos donde se requieren medidas de precisión. La trigonometría se aplica a otras ramas de la geometría, como es el caso del estudio de las esferas en la geometría del espacio.

Posee numerosas aplicaciones, entre las que se encuentran: las técnicas de triangulación, por ejemplo, son usadas en astronomíapara medir distancias a estrellas próximas, en la medición de distancias entre puntos geográficos, y en sistemas globales de navegación por satélites

Historia[editar]

Artículo principal: Historia de la trigonometría

Tablilla babilonia Plimpton 322.

Los antiguos egipcios y los babilonios conocían ya los teoremas sobre las proporciones de los lados de los triángulos semejantes. Pero las sociedades prehelénicas carecían de la noción de una medida del ángulo y por lo tanto, los lados de los triángulos se estudiaron en su medida, un campo que se podría llamar trilaterometría.

Los astrónomos babilonios llevaron registros detallados sobre la salida y puesta de las estrellas, el movimiento de los planetas y los eclipses solares y lunares, todo lo cual requiere la familiaridad con la distancia angular medida sobre la esfera celeste. Sobre la base de la interpretación de una tablilla cuneiforme Plimpton 322 (c. 1900 a. C.), algunos incluso han afirmado que los antiguos babilonios tenían una tabla de secantes. Hoy, sin embargo, hay un gran debate acerca de si se trata de una tabla de ternas pitagóricas, una tabla de soluciones de ecuaciones de segundo grado, o una tabla trigonométrica.

Papiro de Ahmes

Los egipcios, en el segundo milenio antes de Cristo, utilizaban una forma primitiva de la trigonometría, para la construcción de las pirámides. El Papiro de Ahmes, escrito por el escriba egipcio Ahmes (c. 1680-1620 a. C.), contiene el siguiente problema relacionado con la trigonometría:

Si una pirámide es de 250 codos de alto y el lado de su base es de 360 codos de largo, ¿cuál es su Seked?

La solución al problema es la relación entre la mitad del lado de la base de la pirámide y su altura. En otras palabras, la medida que se encuentra para la seked es la cotangente del ángulo que forman la base de la pirámide y su respectiva cara.

Unidades angulares[editar]

En la medición de ángulos y, por tanto, en trigonometría, se emplean tres unidades, si bien la más utilizada en la vida cotidiana es el grado sexagesimal, en matemáticas es el radián la más utilizada, y se define como la unidad natural para medir ángulos, el grado centesimal se desarrolló como la unidad más próxima al sistema decimal, se usa en topografía, arquitectura o en construcción.

• Radián: unidad angular natural en trigonometría. En una circunferencia completa hay 2π radianes (algo más de 6,28).
• Grado sexagesimal: unidad angular que divide una circunferencia en 360 grados.
• Grado centesimal: unidad angular que divide la circunferencia en 400 grados centesimales.
• Mil angular: unidad angular que divide la circunferencia en 6400 unidades.

Transportador en radianes	Transportador en grados sexagesimales
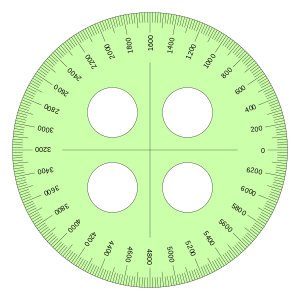Transportador en grados centesimales	Transportador en mil angular

Las funciones trigonométricas[editar]

Artículo principal: Función trigonométrica

La trigonometría es una rama importante de las matemáticas dedicada al estudio de la relación entre los lados y ángulos de un triángulo rectángulo y una circunferencia. Con este propósito se definieron una serie de funciones, las que han sobrepasado su fin original para convertirse en elementos matemáticos estudiados en sí mismos y con aplicaciones en los campos más diversos.

Razones trigonométricas[editar]

El triángulo ABC es un triángulo rectángulo en C; lo usaremos para definir las razones seno, coseno y tangente, del ángulo ${\displaystyle \alpha \,}$, correspondiente al vértice A, situado en el centro de la circunferencia.

• El seno (abreviado como sen, o sin por llamarse "sĭnus" en latín) es la razón entre el cateto opuesto sobre la hipotenusa.

${\displaystyle \operatorname {sen} \,\alpha ={\frac {\overline {CB}}{\overline {AB}}}={\frac {\overline {CB}}{1}}={\overline {CB}}}$

• El coseno (abreviado como cos) es la razón entre el cateto adyacente sobre la hipotenusa.

${\displaystyle \cos \alpha ={\frac {\overline {AC}}{\overline {AB}}}={\frac {\overline {AC}}{1}}={\overline {AC}}}$

• La tangente (abreviado como tan o tg) es la razón entre el cateto opuesto sobre el cateto adyacente.

${\displaystyle \tan \alpha ={\frac {\overline {CB}}{\overline {AC}}}={\frac {\overline {DE}}{\overline {AD}}}={\frac {\overline {DE}}{1}}={\overline {DE}}}$

Representación gráfica[editar]

Representación de las funciones trigonométricas en el plano cartesiano (x,y), los valores en el eje x expresados en radianes.

Razones trigonométricas inversas[editar]

Artículo principal: Inverso multiplicativo

• La cosecante: (abreviado como csc o cosec) es la razón inversa de seno, o también su inverso multiplicativo:

${\displaystyle \csc \alpha ={\frac {1}{\sin \;\alpha }}={\frac {\overline {AB}}{\overline {CB}}}={\frac {\overline {AG}}{\overline {AF}}}={\frac {\overline {AG}}{1}}={\overline {AG}}}$

En el esquema su representación geométrica es:

${\displaystyle \csc \alpha ={\overline {AG}}}$

• La secante: (abreviado como sec) es la razón inversa de coseno, o también su inverso multiplicativo:

${\displaystyle \sec \alpha ={\frac {1}{\cos \;\alpha }}={\frac {\overline {AB}}{\overline {AC}}}={\frac {\overline {AE}}{\overline {AD}}}={\frac {\overline {AE}}{1}}={\overline {AE}}}$

En el esquema su representación geométrica es:

${\displaystyle \sec \alpha ={\overline {AE}}}$

• La cotangente: (abreviado como cot o cta o ctg) es la razón inversa de la tangente, o también su inverso multiplicativo:

${\displaystyle \cot \alpha ={\frac {1}{\tan \alpha }}={\frac {\overline {AC}}{\overline {CB}}}={\frac {\overline {FG}}{\overline {AF}}}={\frac {\overline {FG}}{1}}={\overline {FG}}}$

En el esquema su representación geométrica es:

${\displaystyle \cot \alpha ={\overline {FG}}}$

Normalmente se emplean las relaciones trigonométricas seno, coseno y tangente, y salvo que haya un interés específico en hablar de ellos o las expresiones matemáticas se simplifiquen mucho, los términos cosecante, secante y cotangente no suelen utilizarse

Representación gráfica[editar]

Representación de las funciones trigonométricas inversas en el plano cartesiano (x,y), los valores en el eje x expresados en radianes.

Otras funciones trigonométricas[editar]

Además de las funciones anteriores, existen otras funciones trigonométricas. Matemáticamente se pueden definir empleando las ya vistas. Su uso no es muy corriente, pero sí se emplean, dado su sentido geométrico. Veamos:

El seno cardinal o función sinc (x) definida:

${\displaystyle \operatorname {sinc} \;(x)={\frac {\sin(x)}{x}}}$

El verseno, es la distancia que hay entre la cuerda y el arco en una circunferencia, también se denomina sagita o flecha, se define:

${\displaystyle \operatorname {versin} \;\alpha =1-\cos \alpha }$

El semiverseno, se utiliza en navegación al intervenir en el cálculo esférico:

${\displaystyle \operatorname {semiversin} \;\alpha ={\frac {\operatorname {versin} \;\alpha }{2}}}$

El coverseno,

${\displaystyle \operatorname {coversin} \;\alpha =1-\sin \;\alpha }$

El semicoverseno

${\displaystyle \operatorname {semicoversin} \;\alpha ={\frac {\operatorname {coversin} \;\alpha }{2}}}$

La exsecante:

${\displaystyle \operatorname {exsec} \;\alpha =\sec \alpha -1}$

Funciones trigonométricas recíprocas[editar]

Artículo principal: Función recíproca

En trigonometría, cuando el ángulo se expresa en radianes (dado que un radián es el arco de circunferencia de longitud igual al radio), suele denominarse arco a cualquier cantidad expresada en radianes; por eso las funciones recíproca se denominan con el prefijo arco, cada razón trigonométrica posee su propia función recíproca:

${\displaystyle y=\sin \,x\,}$

y es igual al seno de x, la función recíproca:

${\displaystyle x=\arcsin \;y\,}$

x es el arco cuyo seno vale y, o también x es el arcoseno de y.

si:

${\displaystyle y=\cos x\,}$

y es igual al coseno de x, la función recíproca:

${\displaystyle x=\arccos y\,}$

x es el arco cuyo coseno vale y, que se dice: x es el arcocoseno de y.

si:

${\displaystyle y=\tan x\,}$

y es igual al tangente de x, la función recíproca:

${\displaystyle x=\arctan y\,}$

x es el arco cuya tangente vale y, o x es igual al arcotangente de y.

NOTA: Es común, que las funciones recíprocas sean escritas de esta manera:

${\displaystyle y=\operatorname {arcsin} \;x\quad \longrightarrow \quad y=\sin ^{-1}x\,}$

pero se debe tener cuidado de no confundirlas con:

${\displaystyle y={\cfrac {1}{\sin x}}\quad \longrightarrow \quad y=\csc x}$

Representación gráfica[editar]

Representación de las funciones trigonométricas reciprocas en el plano cartesiano (x,y), como la recíproca del seno, el coseno y la tangente, los valores en el eje y expresados en radianes.

Si aplicamos el criterio para obtener las funciones recíprocas en el sentido estricto, definiendo el arcoseno como la recíproca del seno, el arcocoseno como la recíproca del coseno y el arco tangente como la recíproca de la tangente, lo obtenido es la gráfica de la derecha. Es fácil percatarse que estas representaciones no cumplen la unicidad de la imagen, que forma parte de la definición de función, eso es para un valor de x dado existen un número infinito de valores que son su función, por ejemplo: el arcoseno de 0 es 0, pero también lo son cualquier múltiplo entero de ${\displaystyle \pi }$.

${\displaystyle \arcsin(0)=\pi \;n}$

Para cualquier n número entero.

Dado que la recíproca de una función no tiene que cumplir necesariamente la unicidad de imagen, solo las funciones inyectivas y biyectivas dan funciones recíprocas con esta propiedad, esta situación se repite para el resto de las funciones recíprocas trigonométricas.

Representación de las funciones trigonométricas reciprocas, corregidas.

A fin de garantizar el cumplimiento de la definición de función, en cuanto a la unicidad de imagen, y que por tanto las funciones trigonométricas recíprocas cumplan los criterios de la definición de función, se suele restringir tanto el dominio como el codominio, esta corrección permite un análisis correcto de la función, a pesar de que no coincida exactamente con la reciproca de la función trigonométrica original. Así tenemos que:

La función arcoseno se define:

${\displaystyle {\begin{array}{rccl}\arcsin :&[-1,1]&\to &[-0,5\pi \;,\;0,5\pi ]\\&x&\to &y=\arcsin(x)\end{array}}}$

La función arcocoseno se define:

${\displaystyle {\begin{array}{rccl}\arccos :&[-1,1]&\to &[0\;,\;\pi ]\\&x&\to &y=\arccos(x)\end{array}}}$

La función arcotangente se define:

${\displaystyle {\begin{array}{rccl}\arctan :&R&\to &[-0,5\pi \;,\;0,5\pi ]\\&x&\to &y=\arctan(x)\end{array}}}$

Esta restricción garantiza el cumplimiento de la definición de función, en cuanto a la existencia y unicidad de la imagen, si bien tiene inconvenientes como el no poder comparar el arcoseno y el arcocoseno al estar definidos en codominios diferentes, o el de presentar discontinuidades inexistentes, tanto si se emplean las funciones trigonométricas reciprocas en su forma directa como corregida se ha de ser consciente de ello, y comprender las ventajas e inconvenientes que esto supone.

Funciones trigonométricas inversas recíprocas[editar]

Del mismo modo que las funciones trigonométricas directas recíprocas, cuando el ángulo se expresa en radianes, se denomina arco a ese ángulo, y se emplea el prefijo arco para la función trigonométrica recíproca, así tenemos que:

${\displaystyle y=\csc \,x\,}$

y es igual a la cosecante de x, la función recíproca:

${\displaystyle x=\operatorname {arccsc} \;y\,}$

x es el arco cuya cosecante vale y, o también x es la arcocosecante de y.

si:

${\displaystyle y=\sec x\,}$

y es igual al secante de x, la función recíproca:

${\displaystyle x=\operatorname {arcsec} y\,}$

x es el arco cuya secante vale y, que se dice: x es el arcosecante de y.

si:

${\displaystyle y=\cot x\,}$

y es igual al cotangente de x, la función recíproca:

${\displaystyle x=\operatorname {arccot} y\,}$

x es el arco cuya cotangente vale y, o x es igual al arcocotangente de y.